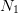 real sequence using a length
real sequence using a length 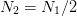 complex FFT. The input real sequence is,
complex FFT. The input real sequence is,
Python Implementation of Real Sequence
Transform using Half-length Complex FFT
John Bryan
We want to transform a length 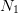 real sequence using a length
real sequence using a length 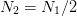 complex FFT. The input real sequence is,
complex FFT. The input real sequence is,
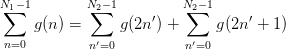 | (1) |
The output complex sequence is
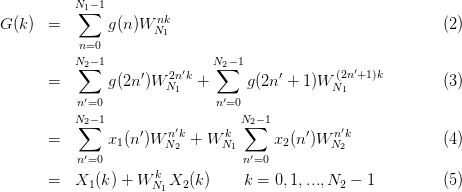
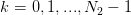 and use
symmetry of real transforms to find G(k) for other values of k in the steps
below.
and use
symmetry of real transforms to find G(k) for other values of k in the steps
below.
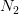 even-indexed values:
even-indexed values:
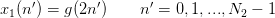 | (6) |
For the 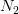 odd-indexed values:
odd-indexed values:
 | (7) |
Form a complex sequence of length 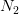 :
:
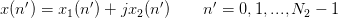 | (8) |
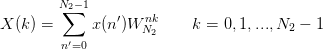 | (9) |
using a 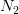 length complex FFT
length complex FFT
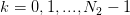 :
:
![{ *
X (k) = 0.5[X (k)+X *((N - k)) ] = 0.5[X (0) + X (0)] if k ≡ 0
1 2 N 0.5[X (k) + X *(N2 - k)] if k ≡ 1, ...,N2 - 1](twelve14x.png) | (10) |
![{
- 0.5j[X (0) - X *(0)] if k ≡ 0
X2 (k) = - 0.5j[X (k )- X *((N2 - k ))N ] =
- 0.5j[X (k) - X *(N2 - k)] if k ≡ 1,...,N2 - 1](twelve15x.png) | (11) |
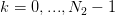 , calculate:
, calculate:
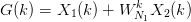 | (12) |
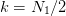 :
:
![G (N1∕2 ) = 0.5([X (0) + X *(0)] + j[X (0) - X *(0)])](twelve19x.png) | (13) |
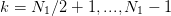 , use symmetry of real transforms:
, use symmetry of real transforms:
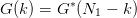 | (14) |